数据库背后的数据结构

2022-02-17 on Liang's blog

来设计一个最简单的数据库

可以通过两个bash函数来实现一个简单的KV存储

#! /bin/bash

db_set() {
  echo "$1,$2" >> database
}

db_get() {
  grep "^$1," database | sed -e "s/^$s1,//" | tail -n 1
}

这里我们用两个函数，一个写入，一个读取，底层存储是一个叫database的文件来做的，每行保存一个KV对，由逗号分开，每次调用写入都会往文件后面append进去一个新的记录，所以如果你对同一个key做过多次更新，那么旧的记录不会删除，每次都会生成新的记录。读取时候会去查到包含key的那些记录，然后返回最后一条记录，也是最新的记录。

$ db_set a 'a'
$ db_set b 'b'
$ db_get a
a
$ db_set a 'A'
$ db_get a
A
$ cat database
a,a
b,b
a,A

在简单数据情况下这个函数的表现还不错，但是在数据库记录很大的时候就表现的很糟糕了。db_get 需要扫描整个数据库问题找到查找的那个key，时间复杂度是O(n)

想要高效的从数据库查找特定的key，我们需要一个索引来帮我们快速查询数据。其背后的基本思想就是存储一些元数据，来帮助我们快速的找到查找的数据，如果我们想要通过不同的方式查找相同的数据，那么则需要在数据的不同字段上建立不同的索引。

索引的建立并不会影响存储数据的内容，它只会影响查找的性能。维护额外的索引也会导致额外的开销，例如写入的性能也会受到索引影响，因为每一个写操作都要去更新对应的索引。

使用Hash表来建立索引

利用hash表来做一个KV存储是最常见的做法，我们这里稍微有一些不同，重新设计一个简单的数据库

  • 它的存储还是按照之前append的方式增量式写入到一个文件中，存储在磁盘上。
  • key和value之间用逗号分割。
  • 同时我们要维护一个hash表，在这个hash表里，它的key是这个数据的key，value是这个数据记录在存储文件中的字节偏移量。
  • 每次append写入新的记录的时候也要去更新这个hash表
  • 查找时候，先在hash表里找到这个key的偏移量，然后读入存储文件，通过偏移量快速找到对应数据的开始位置。

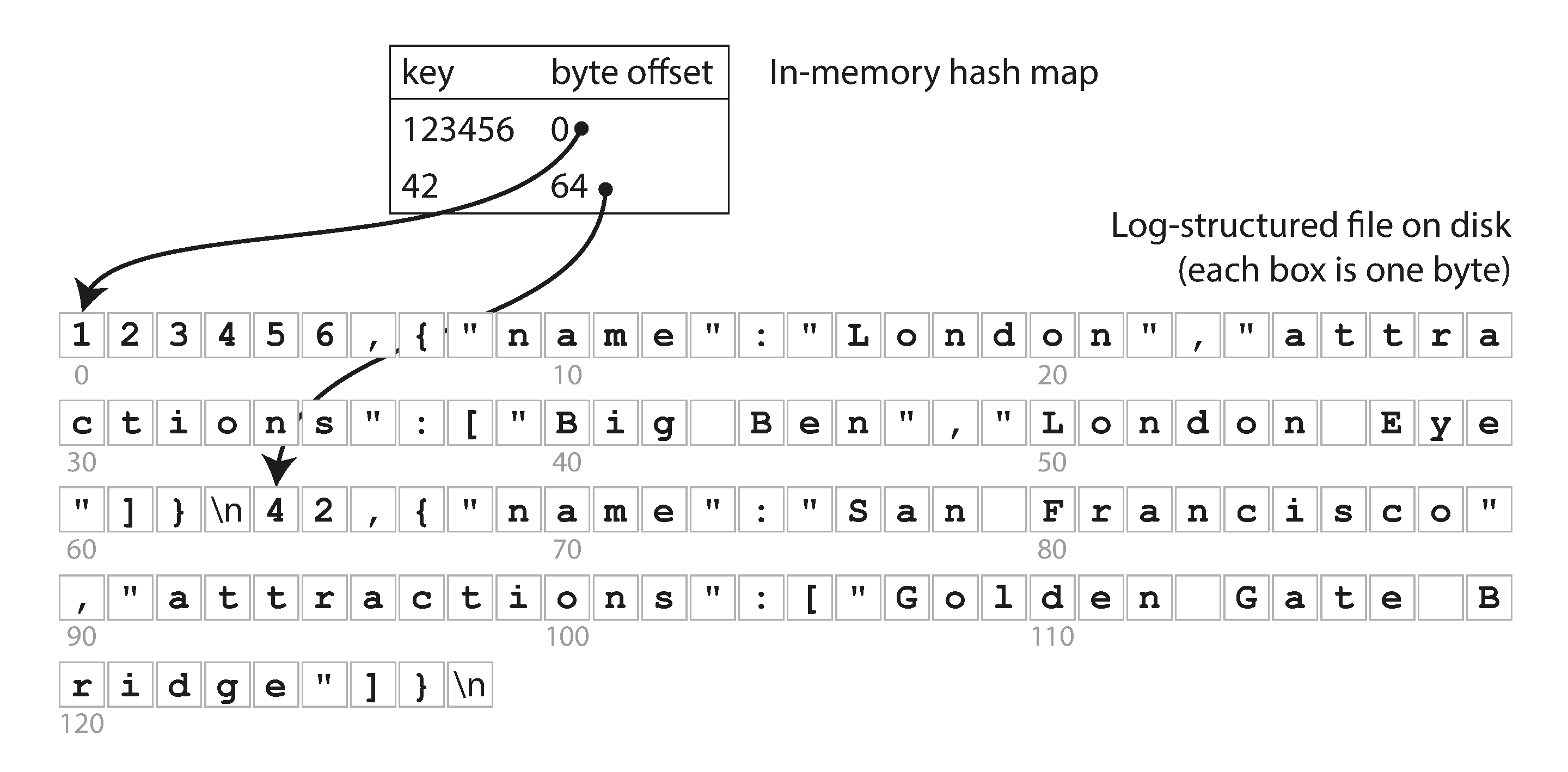
hash table index

这个其实就是Riak的存储引擎Bitcask的基本实现原理

  • Bitcask提供了高性能的读写操作
  • 数据从硬盘加载只需要一次寻址，效率很高
  • 适用于key经常更新的情况，比如记录一个URL被访问的次数，很多的写操作都是在更新同一个key

这里有个问题：数据都存储在一个文件里，而且都是增量式，那么如何避免磁盘空间被占满呢？ 有个很好的解决办法就是把数据分成segment来存储

  • 数据根据指定的大小，切分成一个一个的segment
  • 每个segment存储在一个文件里，每个segment也有自己都应的哈希表
  • 当这个文件达到指定的大小之后，则开始写下一个文件。
  • 然后对之前的这些segment文件进行压缩，压缩的过程就是把重复的key的记录删掉，只保留最新的值
  • 还可以把压缩后的多个文件再合并到一起
  • 压缩和合并的操作可以在后台一个独立线程中执行，不影响数据库对外的服务
  • 完成之后再对新的segment在内存中生成hash表
  • 读请求这个时候可以切换到新的segment文件上，原始的那些文件可以删除。
  • 查询时候先查最新的hash表，如果没有，则查找次新的，以此类推。
  • 压缩和合并的操作会让segment的数量相对非常少，因此这个查找过程也不会查太多的hash表。

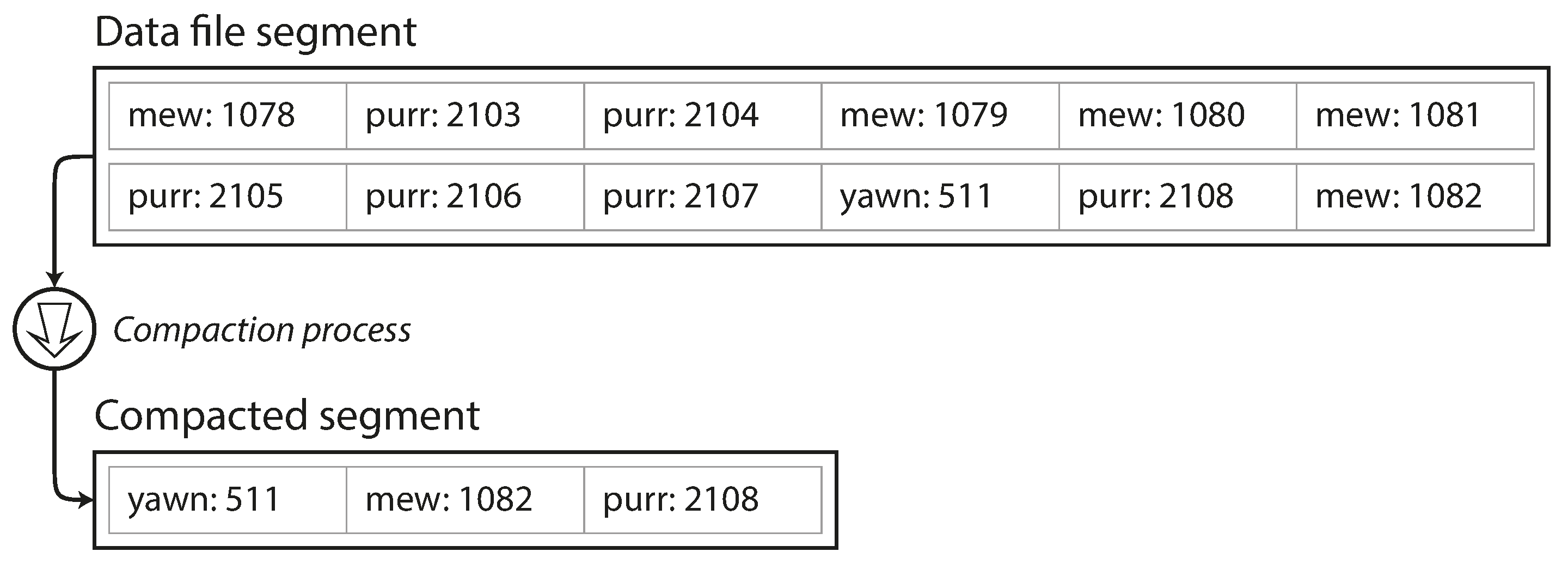压缩一个数据segment，只保留最新的值 压缩一个数据segment，只保留最新的

压缩和合并多个segments 压缩和合并多个segment

实际中还有很多细节来保证这个设计的正常工作

  • 文件格式 - CSV并不是记录数据的最合适格式，计算出String的字节长度后存储在二进制文件中会更快也更简单。
  • 删除记录 - 如果要删除某个记录，需要写入一个特殊的删除记录，当log文件合并在一起的时候，这个记录会告诉合并的代码来删掉这个key的任何记录
  • 数据恢复 - 如果数据库重启了，内存中的哈希表记录就全部都丢了。理论上，可以通过从头到尾读取每个segment的记录来重建哈希表。但是这个可能会花费很长时间。Bitcask是通过从硬盘加载哈希表的快照来恢复的，这样时间更短。
  • 不完整数据 - 如果DB崩溃导致一些数据没有写完全，出现部分数据，可以通过checksums来找到这些不完整的数据，然后忽略掉。
  • 并发控制 - 只保持一个写线程，数据segment只能append写，而且是不可变的。这样可以支持多线程读取。

同时Append-only 被证明是更好的设计， 而不是去修改已有的记录

  • 增量式append写入和segment合并的过程都是顺序的写操作，对于磁盘写入来说比随机写入更快，因为不需要频繁的寻址，尤其是在传统的机械式磁盘中。SSD也更喜欢这种顺序写入
  • 在append only和数据不变的情况下，并发和崩溃恢复会更简单，不需要考虑当修改一个记录到一半的时候crash掉的情况
  • 合并segments可以避免产生更多的数据碎片

但是hash表作为索引实现也有一些限制:

  • hash表都是加载到内存里的，对于非常大的数据，就会占用很多内存。也可以把索引保存在磁盘上，但是性能会大打折扣，因为需要很多随机读取I/O, 同时hash冲突也需要复杂的逻辑来处理。
  • 区间查询的性能不够好，例如想要查询所有在kitty00000到kitty99999的数据，需要在所有的hash表里查找每一个key

SSTable 和 LSM-Tree

在之前的segment里面保存的是一些按照写入顺序排序的KV键值对，对于同一个key来说，后面写入的值最终会替代前面的值，除此之外，不同key之间的顺序其实并不重要。这样的话可以对我们的segment做一些小小的修改：我们要求segment里面的KV对要按照key排序。我们把这个叫做Sorted String Table，或者SSTable。

SSTable对比使用hash表的log segment来说有很多优势：

  • 合并segments非常简单和高效，同时从多个segment文件中读取记录，对比每个文件读入的当前key，根据排序规则找到排序在前的那个key，拷贝到新的segment中，不断重复。这样新生成的那个segment文件也是按照key来排序的。如果一个key在多个文件中都有，那么我们只取最新的segment里面的那个，把老的都丢弃。 merging SSTables
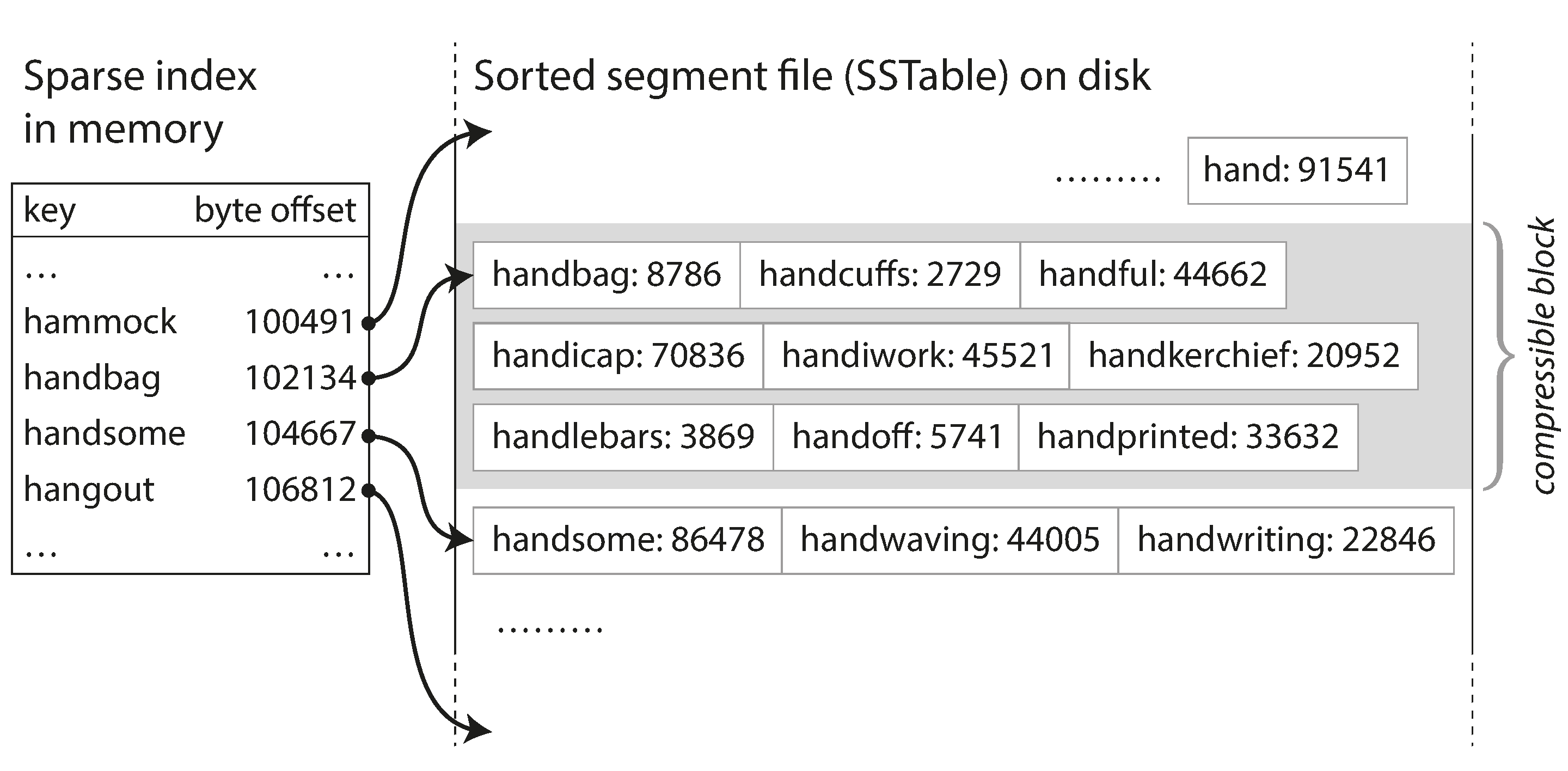
  • 对于查找来说，我们的hash表不需要包含每一个key了，只需要包含少量的key可以，比如每5kb的数据只保存其中一个key和它在segment中的偏移量。在查找时候，根据查找的key和排序顺序找到在hash表里离它最近的前面key和后面那个key，然后去扫描这两个偏移量的区间就可以了。 SSTable and in-memory index
  • 由于查找操作需要去扫描一个区间的数据，我们可以把这个区间的数据放到一起作为一个块压缩，然后写到磁盘上，这样每个hash表中的偏移量就是某个压缩块的起始点，这样可以节约磁盘空间，减少磁盘IO。

可是数据库接受的数据写入请求顺序都是随机的，那么如何在一开始就能够有按照key来排序的segment呢？ 其实在内存中维护一个有序的数据结构是比较简单的，有很多树结构都可以使用，比如红黑树，AVL树，我们可以以任意顺序写入数据，读取时候可以读到排序后的数据。

这样我们的数据库设计看起来是这样：

  • 当写入数据时候，数据写入到在内存中维护的一个平衡树结构，这样的数据结构可以叫做memtable
  • 当memtable中的数据超过一定的阈值之后，比如5M，把它以SSTable的格式写入到磁盘上，这个很容易实现，因为我们可以按照一定顺序从树中读出数据。这样写入磁盘的segment是最新的，在这个过程中，数据库的写入请求会继续写到一个新的memtable中。
  • 对于读请求，首先尝试去memtable中查找，如果没有，再去磁盘上最新的segment中查找，以此类推。
  • 在后台定时的执行合并和压缩segment文件，以节省磁盘空间。

这里有个问题：所以每个segment都对应一个hash table，对吗？

不过这里我们还是能看到一个问题，最新的数据其实都是在memtable里保存着，如果数据库挂了，那么最新写入的数据还没来得及写到磁盘中，就会丢失了。为了避免这个问题，我们可以在磁盘上额外保存一个log文件，每一个写操作到memtable都会立即在这个log里记录，在这个log文件里是不需要排序的，只是用来恢复数据用的。当memtable中的数据写入到磁盘后，对应的log文件也就可以删掉了。

这样的数据库设计其实跟LevelDB和RocksDB的实现原理是一样的，这些KV存储库被设计为嵌入到其他应用程序里工作。LevelDB可以用在Riak里作为存储引擎替换Bitcask，类似的存储引擎同样也被用在Cassandra和HBase里，他们都是受Google的Bigtable的论文启发而设计实现的，在Google的论文中首次提出了SSTable和memtable的概念。

这种索引结构是Patrick O'Neil首次以Log-Structured Merge-Tree的名字提出的，基于这种压缩合并有序文件的存储引擎经常被称作LSM存储引擎。

这里还是有很多细节需要考虑才能让这个设计应用到实际中，例如当要查的key在数据库中不存在的时候会非常慢，因为我们要检查memtable, 然后所有的segments，一一从磁盘中加载然后查找最后都查完发现这个key不存在。为了优化这个场景，数据库通常使用一个叫Bloom Filters的东西来帮助我们检查一个key是否在数据库中。在实际应用中也会有不同的策略来决定key的排序方式和压缩合并的时间，例如常用的选项有size-tiered和leveled，在size-tired下，新的和小的SSTTable会被合并到老的和大的SSTable中去。在Leveled压缩算法下，key的区间范围会被分成更小的SSTable，同时旧的数据会被转移到其他level，这样会让压缩是增量式的，减少磁盘使用。

B-Tree平衡树

LSM索引确实有它的优点，但是实际上应用最广泛的索引数据结构是B-Tree，几乎所有的关系型数据库和很多非关系型数据库都用这个实现。跟SSTable类似，B-tree也按照key的排序保存数据，这样可以提供高效的查找和区间查询，但是B-tree使用了完全不同的设计思想。

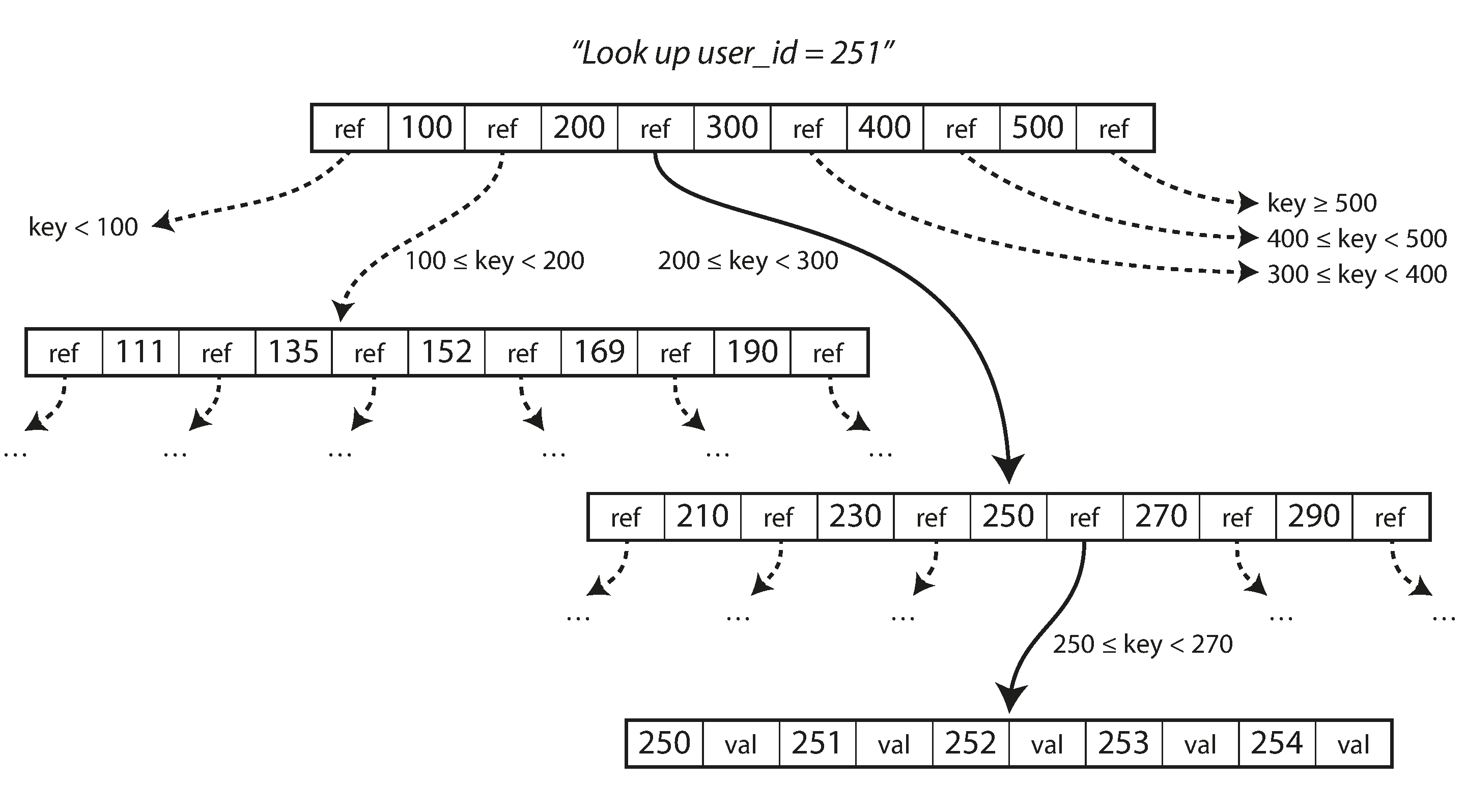
B-tree把数据拆分成固定大小的块或者分页，一般是4KB大小，一次只读写一个块或者分页，每个分页都有自己的地址，其他的分页都可以通过这个地址来引用并找到它，跟指针类似。这样用这些地址引用就可以构建一个包含多个分页的树。 B-tree index

在B-tree里查找一个key

在B-tree里有一个根节点，所有的查询都从这个节点开始，它里面包含了一些keys和child pages的引用，每个child page里包含一系列连续的key，多引用之间的key代表了某一段范围的key的开始和结束，通过那个引用可以找到这个范围内的任意一个key。

当要查询一个key的时候，从根节点开始，找到这个key所属的范围，然后通过这个范围内的引用找到下一个子分页，以此类推，最终找到下面包含这个key的分页中，可以读到它的值。

在一个分页里指向child page的引用的个数叫做分支因子，在上面那个图中，分支因子是6。分支因子取决于用来存储page引用的空间的大小和key起始范围的边界，一般都是几百。

写操作：

  • 更新某个key的时候，要先查找到这个key的分页，修改这个key的值，然后再写回磁盘，其他分页中包含这个修改过的分页的引用依然是有效的。
  • 如果要增加一个新的key，首先要找到这个key最终属于的分页，然后把它加到这个分页里。
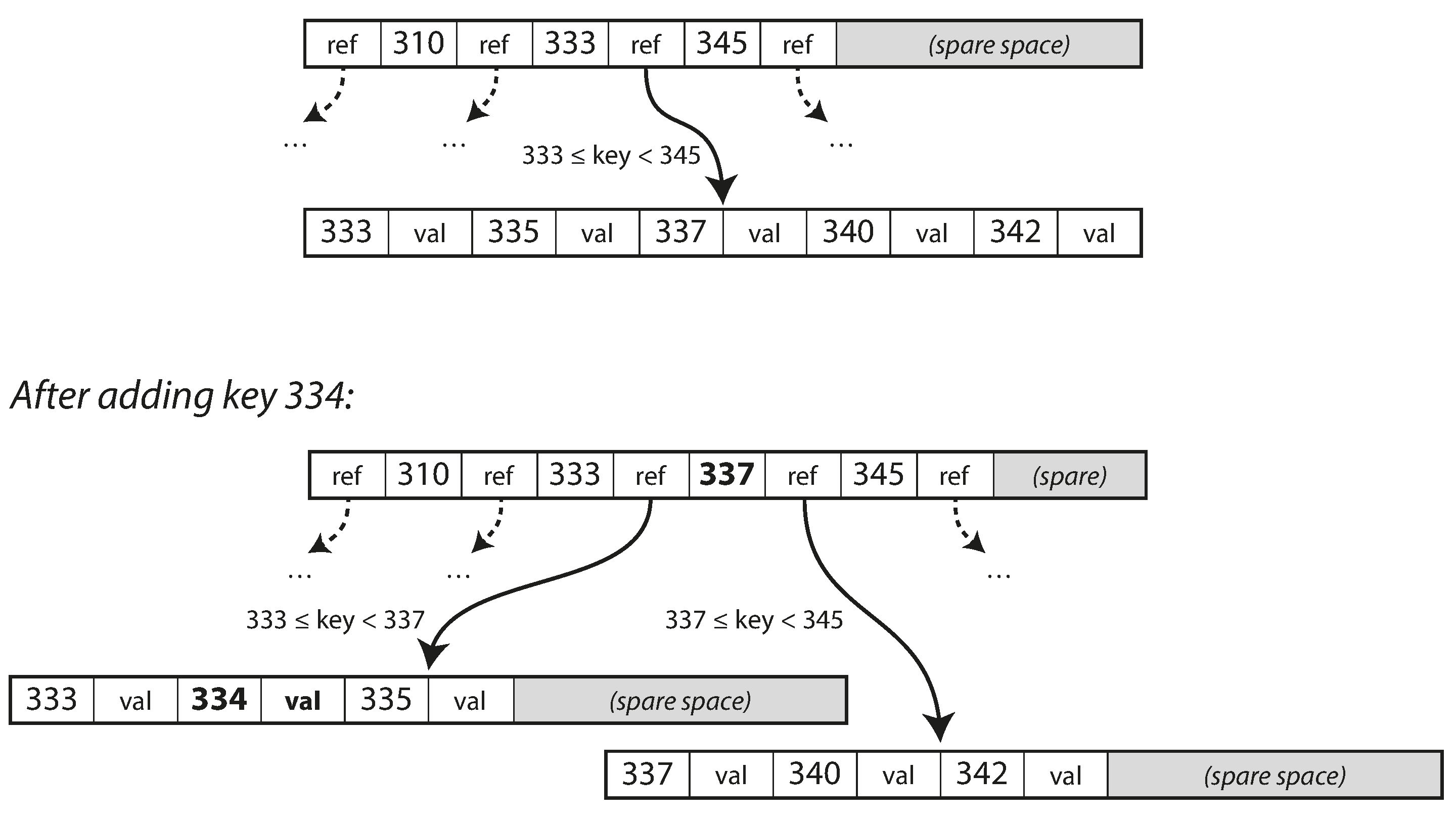
  • 如果这个分页里的空间不够，不能存储新加入的key，那么这个分页会被拆分成2个分页，之前的父分页中会增加新的引用指向新生成的2个分页。 adding new key

这个算法保证树一直是平衡的

  • 一个有n个key的B-tree的深度是O(logn)
  • 对于大部分的数据库来说一个深度为3或4的B-tree基本上足够了，查询不用去找很多层才能找到分页
  • 例如一个4层的树，每个page如果是4KB的话，分支因子为500的时候可以存储多达250TB的数据

由于B-tree在写操作时候需要先找到那个分页，更新后再写回去，对于某些写操作，例如上面的例子，当分页上空间不够的时候，需要拆分成两个，这里涉及到多个分页的多个写操作，当数据库crash的时候这种写操作就很危险，容易丢数据或者产生脏数据。为了解决这样的问题，常用的方式就是使用WAL(write-ahead log)或者叫做redo log。这个log是一个append-only的文件，所有的B-tree的写操作都要先写入这个文件，然后再去更新分页文件。如果数据库崩溃了，当重启之后，这个log会用来恢复数据到之前的状态。

另外在考虑并发控制的时候，经常用 latches (一个轻量级的锁)来保证数据更新中的race condition。

B树的一些优化的设计：

  • 使用写时复制方案，例如LMDB，而不是覆盖页面并维护WAL来支持崩溃恢复。修改的页面被写入到不同位置，并且在树中创建了父页面的版本，指向新的位置，这样对于并发控制也很有用。
  • 通过不存储整个键，而是缩短其大小，来节省也节省页面空间。特别是树内部的页面上，键只要提供足够的信息来充当键范围的边界。这样页面中包含更多键意味着更高的分支因子，允许更少的层级。
  • 分页在硬盘上理论上来说可以存在任何位置，要想将分页在硬盘上连续的保存来获取高效的读取很困难的。相反LSM tree再写入时候可以很容易的维护序列的写入。
  • 额外的指针被加入到树中。例如，每个分页可以有指向它的兄弟分页的指针来快速的扫描兄弟分页的键，而不用跳回父节点再找到兄弟节点。
  • 有一些变种比如fractal tree借用了log structured思想来减少磁盘寻址。

B-tree 和 LSM-tree的比较

一般来说LSM tree写操作更快，而B-tree读更快。

LSM tree的优点： B tree在写操作的时候要写两次，一次写WAL，一次写分页文件（也有可能或许更多，例如碰见需要分页的情况），另外，即使在一个分页上只有一点数据修改，B-tree也要写整个分页。 LSM tree也要写多次，由于不断的数据压缩和合并，这样的写一次导致接下来要再进行多次的写的过程叫做写放大。

参考文献：

  1. «Designing Data-Intensive Applications» 作者: Martin Kleppmann
  2. 文中的图也是从这本书中截取的